Die Bewegung der Planeten ist berechenbar, 

der Mensch ist verantwortbar frei.

_ ELLIPSENZIRKEL

Elliptische Übergangsbögen sind Bestandteil der DIN EN 13803.

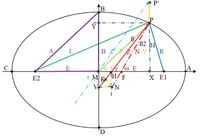
Der Ellipsenzirkel des Benjamin Bramer aus dem Buch von 1623, dem Ziehsohn von Jost Bürgi, einem Mitstreiter im Dienste des Kaisers von Johannes Kepler in dessen Prager Zeit, bei der auch Benjamin anwesend war. Da Kepler erst 1630 verstorben ist, kann es durchaus möglich sein, dass er von diesem Zirkel Kenntnis hatte. Johannes Kepler ist der Erfinder des Zentriwinkels E als „exzentrische Anomalie“ (hier Tau (τ) genannt), er hat damit einen fiktiven Punkt P‘ oberhalb des Stiftes auf Z‘ (türkis) im Abstand A positioniert, um damit die Umlaufzeiten zu bestimmen. Der Zentriwinkel φ, der direkt zum Stift zeigt, ist in den Anwendungen zwar vorhanden, wird aber kaum genutzt. Benjamin Bramer hat den Winkel Tau (τ) als zum Ellipsenzirkel Z (rot) gehörig entdeckt. In der älteren Literatur fehlt teilweise der eigentliche Ort des Winkels, aber er ist immer mal wieder entdeckt worden, wahrscheinlich auch von Kepler, denn er hat noch bis 1630 gelebt. Aber auch 2015 von mir, weil die Ellipse ohne ihn nicht anwenderfreundlich zu bestimmen ist.

__ DIE ELLIPSENGLEICHUNG
X^2 / A^2 + Y^2 / B^2 = 1
_ DIE BRENNPUNKTE E
E = √ [A^2 – B^2]

__ DER WINKEL DES ELLIPSENZEIGERS Τ
X = A COS(τ)
Y = B SIN(τ)
TAN(τ) = AY / BX

__ DER DIFFERENZIALE WINKEL ΔΤ
X + ΔX = A COS (τ + Δτ)
A COS(τ) + ΔX = A COS(τ) – A SIN(τ) Δτ
ΔX = - A SIN(τ) Δτ
ΔY = B COS(τ) Δτ

__ DER ZENTRIWINKEL Φ
TAN(φ) = Y / X = B TAN(τ) / A

_ DER WINKEL DER NORMALEN Ω

Die Normale steht senkrecht auf der Tangente.
TAN(ω) = ΔX / ΔY = A^2Y / B^2X = A TAN(τ) / B = A^2 TAN(φ) / B^2

__ DER DIFFERENZIALE WINKEL ΔΩ
B TAN (ω + Δω) = A TAN (τ + Δτ)
B {TAN (ω) + TAN (Δ ω)} / {1 - TAN (ω) TAN (Δω)} =
A {TAN (τ) + TAN (Δτ)} / {1 - TAN (τ) TAN (Δτ)}
{A TAN(τ) + B Δω} {1 - TAN(τ) Δτ} =
A {TAN(τ) + Δτ} {1 - A TAN(τ) Δω / B}
A TAN(τ) + B Δω - TAN(τ) Δτ {A TAN(τ) + B Δω} =
A TAN(τ) + A Δτ - A TAN(τ) Δω {A TAN(τ) + A Δτ}/ B
{B^2 + A^2 TAN^2(τ)} Δω = AB {1+ TAN^2(τ)} Δτ
{B^2 COS^2(τ) + A^2 SIN^2(τ)} Δω = AB {COS^2(τ) + SIN^2(τ)} Δτ
Δω / Δτ = AB / {B^2 COS^2(τ) + A^2 SIN^2(τ)}

__ DIE KINEMATIK DES ELLIPSENZIRKELS
Die zwei senkrecht zueinander verschiebbaren Schlitten des Ellipsenzirkels haben mit diesen je einen Drehpunkt. Diese Punkte haben voneinander den konstanten Abstand (A – B). Der Stift hat eine Verlängerung des Zeigers mit Abstand B vom Punkt H, welche auch beidseitig möglich wäre. Die Kinematik versucht die notwendigen Glieder und Gelenke zu bestimmen, welche das Zeichnen der Ellipse ermöglichen. Dabei fallen zwei fiktive Punkte auf, die zusätzliche mechanische Grenzen und Berechnungen bestimmen.

___ Die erste Kette:
Das fiktive Gelenk in K liegt auf dem Zirkel mittig zwischen H und V und kreist mit dem ersten Glied im Abstand (A – B) / 2 unter dem negativen Winkel Tau um den Mittelpunkt. Der Zirkel wird dadurch auf andere Weise geteilt als durch die Drehpunkte H und V. Der obere Teil wird unter der X-Achse um ebenfalls (A – B) / 2 unter dem positiven Winkel Tau zu einem zweiten Glied verlängert. Die Drehung des zweiten Gliedes bei gleichem Winkel aber mit umgekehrten Vorzeichen im Gelenk K sowie die gleichen Abstände zur X-Achse bzw. Y-Achse machen es möglich den Anteil unter der X-Achse durch eine Verschiebung auf der X-Achse bzw. auf der Y-Achse zu ersetzen. Am Ellipsenzirkel sind diese drei Varianten augenscheinlich:
1. Verschiebung auf der X-Achse
2. Verschiebung auf der X-Achse und der Y-Achse
3. Verschiebung auf der Y-Achse
Das fiktive Gelenk in K könnte in diesem Fall tatsächlich zu einem realen werden und mit dem Mittelpunkt mechanisch verbunden sein, dann könnte sogar einer der Schlitten entfallen.

__ Die zweite Kette:
Das fiktive Gelenk in N umkreist den Mittelpunkt im doppelten Abstand, so dass K mittig auf der gleichen Strecke zum Mittelpunkt liegt. Als zweites Glied der Kette wird damit die Normale gefesselt.
4. Verschiebung auf der X-Achse und der Y-Achse

_ DIE BOGENLÄNGE ΔU1
Die Kette besteht aus Radius B dem Glied des Ellipsenzirkels oberhalb der X-Achse und der Verschiebung von Punkt H als Ersatz für die Verschiebungen unterhalb der X-Achse.
H = (A – B) COS(τ)
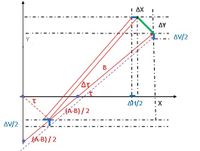
Δu = √ [(ΔX – ΔH) ^2 + ΔY^2] + ΔH
Δu1 / Δτ = B + (A – B) SIN(τ)
Δu0° = B Δτ
Δu90° = A Δτ
u1 = τB + (A – B) (1 - COS(τ))
U1 = 2πB + 4 (A - B)

__ DIE BOGENLÄNGE ΔU2
Die Kette besteht aus dem um M kreisenden Radius 0,5 (A – B) und dem Glied des Ellipsenzirkels oberhalb des Punktes K (für den 1. Quadranten).
{E03_DxDy}
V = (A – B) SIN(τ)
ΔV hat keinen direkten Einfluss auf die Bogenlänge, weil die Verschiebung unterhalb der X-Achse stattfindet und muss deshalb wieder abgezogen werden.
Δu = √ [(ΔX – 0,5 ΔH) ^2 + (ΔY + 0,5 ΔV) ^2] + 0,5 (ΔH – ΔV)
Δu2 / Δτ = 0,5 (A + B) + 0,5 (A – B) (SIN(τ) - COS(τ))
Δu0° = B Δτ
Δu90° = A Δτ
u2 = 0,5τ (A + B) + 0,5 (A – B) (1 - COS(τ) - SIN(τ))
U2 = π (A + B)


__ DIE BOGENLÄNGE ΔU3
Diese Variante ist das Äquivalent der ersten Variante mit A statt B und V statt H.
Δu = √ [Δx^2 + (Δy + Δv) ^2] - Δv
Δu = √ [A^2 SIN^2(τ) + A^2 COS^2(τ)] – (A – B) COS^2(τ)
Δu3 / Δτ = A – (A – B) COS(τ)
Δu0° = B Δτ
Δu90° = A Δτ
u3 = τA – (A – B) SIN(τ)
U3 = 2πA – 4 (A – B)

_ DIE KURVEN DES LAUFENDEN UMFANGS U
Für B = 1 und A = 1,5: Tau = 0° bis 90°

___ DIE KURVEN DES GESAMTEN UMFANGS U

Für B = 1 und A = 1 bis 2

__ MODELLE DER BOGENLÄNGE EINER ELLIPSE

U1 = 2πB + 4 (A – B) diese Bogenlänge ist zu groß!

U2 = π (A + B) hier wird das Original umgekehrt das Kleine läuft auf dem Großen!

U3 = 2 πA– 4 (A – B) diese Bogenlänge ist zu klein!

_ DIE NORMALE
Das Gelenk in N als Verlängerung von MK und doppelt so weit von M entfernt:
NX = H
NY = V
Und damit die Radien:
MN = (A – B)
NP = N = √ [(X – H) ^2 + (Y + V) ^2]
N = √ [A^2 SIN^2(τ) + B^2 COS^2(τ)]

__ DIE BOGENLÄNGE ΔU4

Eine Kurbel im fiktiven Punkt N trennt zwei rotierende Glieder einer kinematischen Kette, die nachfolgende Verschiebungen unterliegt:
Δu4 = ΔH – ΔV + N Δω
Δu4 / Δτ = (A – B) (SIN(τ) – COS(τ))
+ √ AB [B^2 COS^2(τ) + A^2 SIN^2(τ)] / (B^2 COS^2(τ) + A^2 SIN^2(τ))
Δu4 / Δτ = AB / √ [B^2 COS^2(τ) + A^2 SIN^2(τ)] + (A – B) (SIN(τ) – COS(τ))
Δu0° = B Δτ
Δu90° = A Δτ

__ DIE BOGENLÄNGE ΔU5 DES RADIUS
Bronstein Semndjajew Taschenbuch der Mathematik
Δu = R Δω
Δu5 / Δω = A^2B^2 √ [X^2 /A^4 + Y^2 / B^4] ^3
Δu5 / Δτ = N
Δu5 / Δτ = √ [B^2 COS^2(τ) + A^2 SIN^2(τ)]
Δu0° = B
Δu90° = A
Hier fehlt zumindest die Verschiebung des Fußpunktes.

__ DIE DIFFERENZIALEN DES UMFANGS
Δu1 / Δτ = B + (A – B) SIN(τ)
Δu2 / Δτ = 0,5 (A + B) + 0,5 (A – B) (SIN(τ) – COS(τ))
Δu3 / Δτ = A – (A – B) COS(τ)
Δu4 / Δτ = AB / √ [B^2 COS^2(τ) + A^2 SIN^2(τ)] + (A – B) (SIN(τ) – COS(τ))
Δu5 / Δτ = √ [B^2 COS^2(τ) + A^2 SIN^2(τ)]
Für B = 1 und A = 1,2: Tau = 0° bis 90°

__ FLÄCHENVERGLEICH

F1 = 0,5τAB + B (A – B) COS(τ) SIN(τ)
BOM = 0,5AB ARCCOS (X / A)
B0M = 0,5AB ARCCOS (COS(τ))
BOM = 0,5τAB
Ein Ellipsensektor mit folgenden Koordinaten:
B(A; 0)
0(0; 0)
M(X; Y)
A = 1,2 B = 1 Tau = 0° bis 90°
{E09_FlBo}
Der Vergleich kann auch mit dem Winkel ω erfolgen, aber X / A war leichter in COS(τ) umzuwandeln.
τ = ARCTAN (B TAN(ω) / A)
f = 0,5AB ARCTAN (B TAN(ω) / A)
+ AB^2 (A – B) COS(ω) SIN(ω) / (A^2 COS^2(ω) + B^2 SIN^2(ω))
BOM = 0,5AB ARCTAN (B TAN(ω) / A)
A = 1,2 B = 1 Omega = 0° bis 90°
{E10_FoBo}
Auch als Funktion in Abhängigkeit von Omega, die Differenzen bleiben natürlich.

__ DIE 3-DIMENSIONALE ELLIPSE
Für die 2-dimensionale Ellipse in Großbuchstaben:
Z: √ [ΔX^2 + ΔY ^2]
Für die 3-dimensionale Ellipse in Kleinbuchstaben:
D: √ [Δx^2 + Δy ^2 + Δz^2]
Hiermit werden Diagonalen bestimmt, aber keine Bogenlängen, denn die machen einen Umweg!

__ DIE KOORDINATEN
(x^2 + z^2) / A^2 + y^2 / B^2 = 1
, y = Y
, x^2 = B^2 – y^2
Bei gleicher Länge der Diagonale
, z^2 = X^2 + Y^2 - B^2
, x = B COS(τ)
, y = B SIN(τ)
, z = E COS(τ)

__ DIE DIFFERENZIALE
Δx / Δτ = - B SIN(τ)
Δy / Δτ = B COS(τ)
Δz / Δτ = - E SIN(τ)

__ DIE KURVEN DER DIFFERENZIALEN
Für B = 1 und A = 1,2: Tau = 0° bis 90°

__ DIE BOGENLÄNGEN
Herkömmlich: ΔuZ = √ [ΔX^2 + ΔY^2]
ΔuZ = √ [(ΔX – i ΔH) ^2 + (ΔY + i ΔV) ^2] + i (ΔH – ΔV)
Herkömmlich: ΔuD = √ [Δx^2 + Δy^2 + Δz^2]
ΔuD = B Δτ - Δz
Rollt man den Mantel des Rohres ab, bleibt eine 2-dimensionale Kurve übrig.

_ DIE GESCHWINDIGKEIT
Fakt ist, dass hier die Gleichzeitigkeit der Bewegungen berücksichtigt wird, und bei konstanter Drehgeschwindigkeit ergibt sich dann:
V = 2π (0,5 (A + B) + 0,5 (A – B) (SIN(τ) - COS(τ))) / D

_ DIE WEITEREN ABSTÄNDE
L = √ [(E + X) ^2 + Y^2]
P = √ [X^2 + Y^2]
R = √ [(E - X) ^2 + Y^2]

__ DIE BESTÄTIGUNG DER GLEICHHEIT DER WINKEL ß
2 LN‘ COS (ß) = L^2 + N‘^2 – (E + F) ^2
2N COS (ß) = ((E + X) ^2 + Y^2 + (X - F) ^2 + Y^2 – (E + F) ^2) / √ [(E + X) ^2 + Y^2]
2 NR COS (ß1 + ß2) = N‘^2 + R^2 – (E – F) ^2
2 N COS (ß) = ((E - X) ^2 + Y^2 + (X - F) ^2
+ Y^2 – (E – F) ^2) / √ [(E - X) ^2 + Y^2]
ß = ß1 + ß2
(((E + X) ^2 + (B^2X / A^2) ^2 + 2Y^2 – (E + X (1 - B^2/ A^2)) ^2)) ^2 ((E - X) ^2 + Y^2) =
(((E - X) ^2 + (B^2X / A^2) ^2 + 2Y^2 – (E – X (1 - B^X / A^2)) ^2)) ^2 ((E + X) ^2 + Y^2)
0 = A^2B^4 – B^4 X^2 - A^4B^2 + A^2B^2X^2 - A^2B^2X^2 + A^2B^2E^2 + B^4X^2
0 = 0
Qed